Measures of Central Dispersion

Jun 20, 20227 min read

Updated: Sep 16, 2024

Measures of Central tendency are called averages of first order, but these are not sensitive to the variability among the data. Two distributions may have same Mean, Median and Mode but the variability among the data in two distributions may be quiet different.

For example consider two groups ‘A’ and ‘B’ as

Computing Averages we get,

It is clear that Group A and Group B have same values of Mean. Median and Mode, but careful perusal of data in both the groups show that the values in Group B are much more widely scattered than the values in group A

Sometimes the two series may have similar formation but their measurement of Measures of Central Tendency may be different.

The series have entirely different average but the same formation. Clearly measurement of central tendency do not indicate how the individual values in the distribution differ from each other or from the central value.

When extent of variation of individual values in relation to other values or in relation to the central value is large, the Measures of Central Tendency fail to represent the series fully.

The Measures of Dispersion (or variability) coupled with the Measures of Central Tendency gives a fairly good idea (not the full idea) about the nature of the distribution.

To have a complete idea about the nature of data Moments and Kurtosis must also be measured.

Dispersion is the spread or scatter of values from the Measure of Central Tendency

A Measure of Dispersion is designed to state the extent to which individual observations (or items) vary from their average. Here we shall account only the amount of variation but not the direction.

D.C. Brooks define dispersion as “Dispersion or spread is the degree of scatter or variation of variable about the central value”.

Measures of Dispersion are called Averages of Second order because they are based on the deviations of the different values from the mean or other measures of central tendency which are called averages of First order.

Objectives of Dispersion

To know the average variation of different values from the average of a series.
To know about the composition of a series or the dispersion of the values on either sides of the central tendency.
To know the range of values.
To compare the disparity between two or more series expressed in different units in order to find out the degree of variation.
To know whether the Central Tendency truly represent the series or not. If the dispersion is more the central tendency do not represent the series.

Importance of Dispersion

Conclusion drawn from the central tendency carries no meaning without knowing variation of various items of the series from the average.
Inequalities in the distribution of wealth and income can be measured in dispersion.
Dispersion is used to compare and measure concentration of economic power and monopoly in the country.
Dispersion is used in output control and price control.

Characteristics of Good Dispersion

It should be simple to understand and easy to calculate.
It should be rightly defined.
It should be based on the all items of the series.
It should not be unduly affected by the extreme items of the series.
It should be least affected by the sample fluctuations.
It should be amenable to the further algebraic treatment.

Merits of Dispersion

They indicate the dispersal character of the statistical series.
They speak the dependability or reliability of the average value of a series.
The enable the statistician in comparing between two or more statistical series with regard to the character of their uniformity or consistency or equitability.
They enable the one in controlling the variability of a phenomenon under his purview
They facilitate in making further statistical analysis of the series through devices like co-efficient of Skewness, co-efficient of Kurtosis, co-efficient of correlation, variance analysis etc.
They supplement Measures of Central Tendency in finding out more and more information related to the nature of a series

Demerits of Dispersion

They are liable to misinterpretations and wrong generalization by a statistician of a biased character.
They are liable to yield inappropriate results as there are different methods of calculating the dispersion.
Except one or two, most of the dispersion involve complicated process of computing.
They by themselves can not give any idea about the symmetrical or skewed character of a series.
Like measures of central tendency, most of the measures of dispersion do not give a convincing idea about a series to a layman.

Difference b/w Absolute & Relative Measures

An absolute Measure of Dispersion is expressed in terms of the units of the measurement of the variable. The relative measure of dispersion generally known as co-efficient of dispersion is expressed as a pure number independent of the units of measurement of the variable.

The main disadvantage of the absolute measure of dispersion is that it can not be used to compare the variability of two expressions measured with different units.

Range

It is defined as difference between extreme value in the distribution, i.e.,

Range = Largest Value in the Distribution - Smallest Value in the Distribution

In case of continuous frequency distribution range is calculated by any one of the following two methods.

By subtracting the lower limit of the lowest class from the upper limit of the highest class OR By subtracting the mid-value of the lower from mid value of the highest class.

Important

In calculation of Range only the values of the variable are taken in to account and the frequencies are completely ignored.
Open ended classes have no Range since they have no highest and lowest value.
Some times, variability of two series is measured by Range only though it is a rough measure of variability.

Coefficient of Range

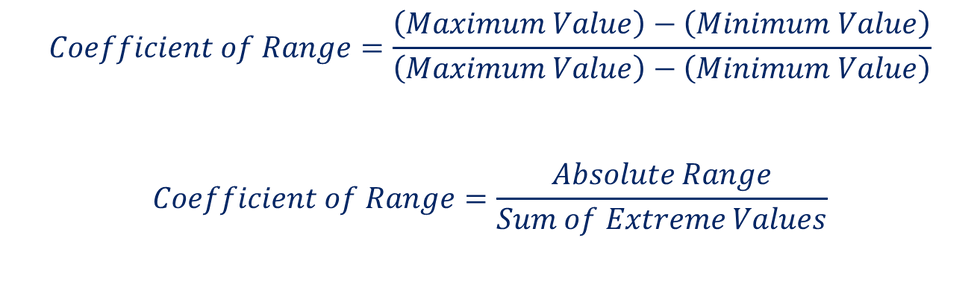
Inter-quartile Range

Percentile Range

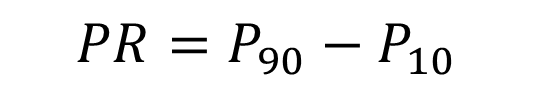
Quartile Deviation

Coefficient of Quartile Deviation

For Symmetric Distribution

For Asymmetric Distribution

Merits of Quartile Deviation

Simple to understand and easy to compute.
Not affected by extreme values.
Computed even if distribution has unequal intervals.
Computed in case of open ended intervals

Demerits of Quartile Deviation

It is not based on the all observations of the series because it does not take frequencies below the lower quartile and above the upper quartile into consideration.
Not amendable to algebraic treatment.
Affected by sample fluctuations.
It is a distance on the scale and is not a measure from average. Therefore, it fails to show variations around an average.

The quartile deviation, as a measure of dispersion, is mainly employed in open ended distributions. In many situations, we encounter such distributions because of the need to keep certain information confidential.

Mean Deviation

Mean deviation (also called Average Deviation) is defined as the arithmetic mean of the absolute deviations of all the values from their Mean or Median or Mode.

Steps to Calculate Mean deviation in Individual Values (or Observations)

In case of individual observations, the following steps are involved in the calculation of Mean Deviation

Calculate the Mean or Median of a given series.
Write down the deviations (dxi)of each item (xi ) either from the Mean or the Median without considering the sign.
Sum up the deviations disregarding the signs
Divide the total of the deviations by the number of observations and the resulting value is the Mean Deviation.

Steps to Calculate Mean deviation in – Discrete Series

In case of discrete series, the following steps are involved in the calculation of Mean Deviation;

Calculate the Mean or Median of a given series
Write down the deviations (dxi)of each item (xi ) either from the Mean or the Median without considering the sign.
Multiple the deviations by frequencies
Find sum of the products so obtained.
Divide the sum of products by the total frequency and the resulting value is the mean deviation. Expressed as a formula form

Coefficient of Mean Deviation

It is a relative measure of dispersion and is computed by the following formula;

Standard Deviation

Standard Deviation is the most important, the most reliable and the most widely used measure of dispersion. The term ‘standard’ is assigned to this measure of variation probability because of the following reasons.

It is the most commonly used and is the most flexible in terms of variety of applications of all measures of variation.
The area under any symmetrical curve rather normal curve remains the same with in a fixed number of standard deviations from the Mean on either side of it, e.g., in any normal curve area with in Mean ± standard deviation is always 68.27% of the total area and the area is 95.45% of the total area with in mean ± 2 standard deviation.
The sum of squares of the deviations about the Mean is the least as compared to the sum of the squares of the deviations about the Median or Mode, therefore, root Mean square deviation about the Mean is the least.

It is most important of all the measures of dispersion because it is used in many other statistical operations, e.g., sampling techniques, correlation and regression analysis, finding co-efficient of variation, skewness, kurtosis, etc. standard deviation is also called ‘Mean Error’ or ‘Mean Square Error’ or ‘Root-Mean Square Deviation’ Unlike the Mean Deviation, which may be calculated around any average, the standard deviation is always computed around the Mean. It is the square-root of the Arithmetic Mean of the squared deviations of all values from their Mean.

Standard Deviation is Used When Data is Approximately Normal or Normal