
Index Numbers are the devices which measure the relative change in the level of a phenomenon with respect to time, geographical location or some other characteristics.
Index numbers are basically used in measuring relative changes and generally expressed in percentage form.
May be defined as the device which enables us to combine the variations in different series with a view to obtain a figure that faithfully represents the net result of the change in constituent elements.
For calculating index numbers we consider two time periods.
Base Period
Base Period is the point of time with which all later changes are compared, i.e., the period w.r.t which the change is measured
Current Period
Current period is the period of time in which change is measured considering the prices in the base period as standard
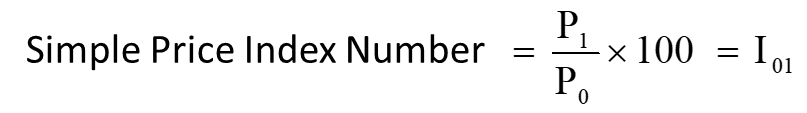

Important
Variables (i.e., price production, consumption, etc.) are suppose to remain constant over the base period. Base period and current period are normally taken as one year, so we call them as Base year and current year. When the comparison is made in respect of prices the index numbers is called Index number of prices or price index number or price relative or price index.

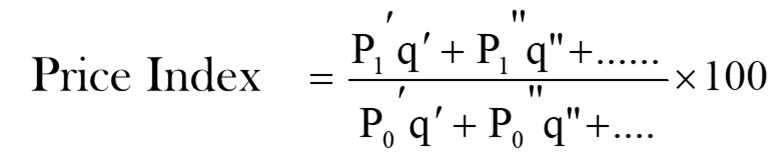
If we can consider only the quantities produced or consumed in the current year and Base year, the Index number is called ‘Quality Index number’. The sum of the products of quantities purchased with their respective prices per unit in any period is called True value for that period.
There are two types of weights:
Quantity Weight: Symbolized by ‘q’, means the amount of a commodity produced, distributed or consumed in some time period.
Price Weight: Symbolized by ‘p’, means the price per unit of a commodity produced, distributed or consumed in some time period.
Simple or Composite Index Numbers
When the variation in the level of single item is being studied, the index number is called uni variate or single index number. If the changes in the average level of various items is being studied together, this index number would be called a composite index number.
Methods of construction of Price Index Numbers
Simple aggregate of Prices.
Weighted aggregate of Prices
Simple arithmetic mean of Price Relative.
Simple geometric mean of Price Relative.
Weighted arithmetic mean of Price Relative.
Weighted geometric mean of Price Relative.
Family Budget Method.




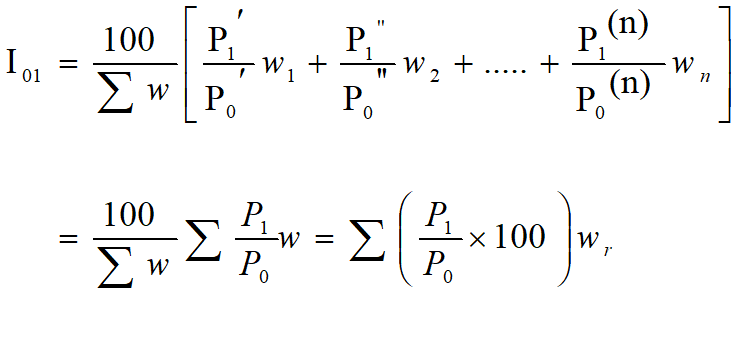


Laspeyre’s Price Index Number
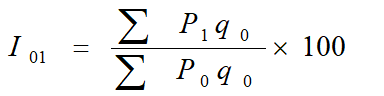
Passche’s Price Index Number

Dorbish Bowley’s Index Number
The Arithmetic Mean of Laspeyre’s Index Number and Pasche’s Index Number is known as Dorbish Bowley’s or simply Bowley’s index number

If the quantity index number is prepared by using Laspeyer’s method, the base year prices will be used as weights:

In Paschey’s method current year’s price are used as weights

Marshal – Edgeworth’s Index Number
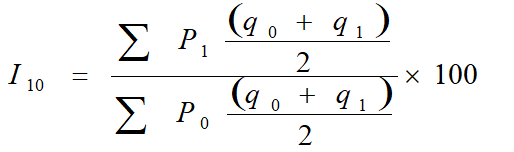
Kelly’s Method

Where q is the quantities of the year selected as base
Comparison Between Laspeyre’s Index Number and Paasche’s Index Number

Comments